數位訊號處理第3部分-傅立葉變換

Published by Tiberia Todeila at 2022.01.25

硬體

Arduino Uno
用於Arduino的MAX9812L駐極體麥克風感測器板

軟體

Arduino IDE
MATLAB

步驟1：傅立葉變換簡介

我們首先瞭解一下相關定義。訊號是“傳遞某種現象的行為或屬性資訊的一種函數。” 時域表示訊號的幅度是如何隨時間變化的，而頻域則表示隨頻率變化的幅度頻。讓我們再次看一下心電圖（ECG）示例。心電圖顯示的是重複的訊號波，可以觀察到這些訊號波的特徵是如何隨時間變化的（即訊號是如何演化的）。很難對一段較長時間內記錄的ECG的每個重要成分都進行分析。在這種情況下，您可以將訊號轉換到頻域，並觀察在特定時間間隔內重複的每個分量。這就是傅立葉變換的來歷。

FT也會在圖像和視訊壓縮中用到。例如，jpg 和 mp3是使用了快速傅立葉變換（FFT）演算法的圖像和聲音的數位格式。由於必須使用模數轉換器將每個連續的類比訊號轉換為數位訊號，所以需要以特定頻率對這些訊號進行採樣。這樣，我們可以利用離散傅立葉變換獲取離散訊號。

傅立葉級數的有趣之處在於，每個波形都可以寫成正弦和余弦的總和，但是具有離散頻率分量。使用TF，我們可以將波形分解為正弦波。

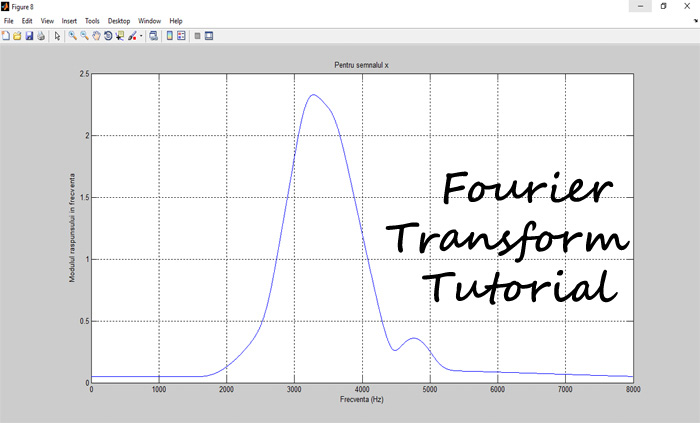
讓我們看一下由多個正弦波組成的訊號。該圖顯示了一個來自現實世界的具有多個頻率分量的訊號：

圖1：初始訊號

我們將會通過下面的所有步驟來逐步添加正弦波，以確定該訊號是如何形成的。

f1 = 1;
f2 = 0.5;
f3 = 1.5;
f4 = 4;
t = 0:0.01:4;
A1 = 0.5;
A2 = 2.5;
A3 = 7.5;
A4 = 3.5;

x1 = A1*sin(2*pi*f1*t)
x2 = A2*sin(2*pi*f2*t)
x3 = A3*sin(2*pi*f3*t)
x4 = A4*sin(2*pi*f4*t)

x = x1 + x2+ x3+ x4

添加到圖形中的第一個訊號如下：

figure %Figure 2
subplot(2,1,1)
plot(t,x,t,x1)
subplot(2,1,2)
plot(t,x1)

圖2：形成圖1訊號的第1步

在圖2中，正弦波（底部）被繪製在初始訊號（頂部）中。初始訊號還包含許多其它訊號。我們將嘗試獲取頂部圖形中的藍色訊號，證明任何訊號都可以表示為一些正弦訊號之和。

figure %Figure 3
subplot(3,1,1)
plot(t,x,t,x1+x2)
subplot(3,1,2)
plot(t,x2)
subplot(3,1,3)
plot(t,x1+x2)

以下訊號應該盡可能接近原始訊號。在隨後的每個圖中將具有以下三個子圖：

subplot(3,1,1)：在同一座標圖中繪製兩個圖形，藍色表示初始訊號，由不同頻率的正弦波疊加而成，綠色表示獲得原始訊號之前的所有步驟中所添加訊號的總和。
subplot(3,1,2)：當前步驟中所添加的訊號，由另一個幅度和頻率來表達。
subplot(3,1,3)：訊號總和 – subplot(3,1,1) 中的綠色訊號，沒有重疊部分。

圖3：形成初始圖像的第2步

從圖3中可以看出，訊號已經開始形成初始訊號的波形。在subplot(3,1,3)中，您可以觀察到形狀由於添加了更多的訊號而發生了變化。從這一步開始，訊號不再是標準的正弦曲線形狀。

figure %Figure 4
subplot(3,1,1)
plot(t,x,t,x1+x2+x3)
subplot(3,1,2)
plot(t,x3)
subplot(3,1,3)
plot(t,x1+x2+x3)

圖4：形成原始訊號的第3步

在圖4中，我們可以觀察到subplot (3,1,3)的訊號幅度是如何演變的。A3 = 7.5表明，當添加多個訊號時，所得訊號的幅值是由每個訊號的幅值相加得到的。

figure %Figure 5
subplot(3,1,1)
plot(t,x,t,x1+x2+x3+x4)
subplot(3,1,2)
plot(t,x4)
subplot(3,1,3)
plot(t,x1+x2+x3+x4)